library(tidymodels)
library(tidyverse)
library(performance)
library(here)Fitting
This exercise is the third in the flu analysis series. This page will use the flu analysis data to create and fit models for the two main outcomes (body temperature and nausea) against one predictor (runny nose) and a full model with all symptoms.
Load packages
Load data
Load the cleaned data from the data folder. Reassign as flu.
#load data
filelocation <- here("fluanalysis", "data", "cleandata.rds")
load(filelocation)
#reassign as flu
flu <- cleandataFit linear model: RunnyNose
First, we will create the univariate linear model of runny nose predicting body temperature
lm_mod <- linear_reg() #set linear regression
RNlm_fit <- lm_mod %>%
fit(BodyTemp ~ RunnyNose, data = flu) # create fitted linear model
tidy(RNlm_fit) #produce summary of fitted model# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 99.1 0.0819 1210. 0
2 RunnyNoseYes -0.293 0.0971 -3.01 0.00268The fitted model has produced a linear equation of BodyTemp = -0.2926(RunnyNoseYes) + 99.14. This would indicate that having a runny nose actually predicts a lower body temperature.
Predicting from model
Next, we can try predicting from the linear model. This code follows the “Getting Started” code from the tidymodels website. We will use median body temperature as our predicted outcome based on runny nose as the predictor.
new_points <- flu %>%
expand.grid(BodyTemp = 98.50, #median body temperature found during exploration portion
RunnyNose = c( "Yes", "No")) #create expanded dataframe
median_predict <- predict(RNlm_fit, new_data = new_points) #predicts output values from the expanded dataframe
tidy(median_predict) #summary table of predictionWarning: Data frame tidiers are deprecated and will be removed in an upcoming
release of broom.# A tibble: 1 × 13
column n mean sd median trimmed mad min max range skew
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 .pred 56 99.0 0.148 99.0 99.0 0.146 98.9 99.1 0.293 -1.46e-13
# … with 2 more variables: kurtosis <dbl>, se <dbl>conf_int_pred <- predict(RNlm_fit,
new_data = new_points,
type = "conf_int") #confidence intervals for prediction
plot_data <- new_points %>%
bind_cols(median_predict) %>%
bind_cols(conf_int_pred) # create new data set with prediction and confidence intervalsTo view the output easier, we will plot the predicted points using ggplot
ggplot(plot_data, aes(RunnyNose))+
geom_point(aes(y = .pred))+ #predictions on the y axis
geom_errorbar(aes(ymin = .pred_lower,
ymax = .pred_upper), #produces error bars
width = 0.5) +
labs(y = "Body Temperature")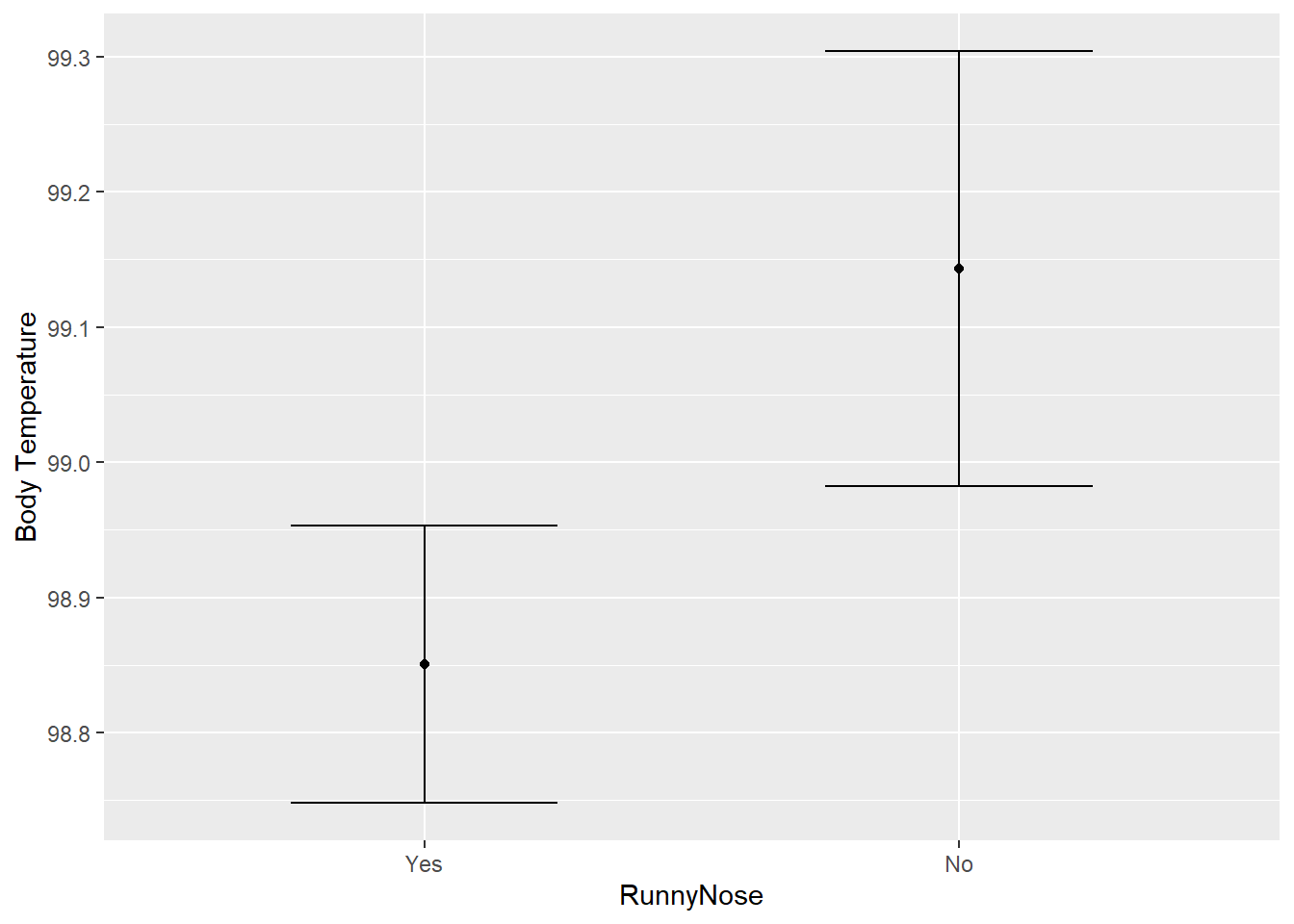
We can see the predicted median body temperature based on having a runny nose is 98.85 degrees and 99.15 if you don’t have a runny nose. Interesting!
Fit linear model: All symptoms
Next, we will create a fitted linear model using all symptoms as predictors.
lm_mod <- linear_reg()
ASlm_fit <- lm_mod %>%
fit(BodyTemp ~ ., data = flu) #use all symptoms (including nausea) as predictors
tidy(ASlm_fit) #summary of fit# A tibble: 34 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 97.9 0.304 323. 0
2 SwollenLymphNodesYes -0.167 0.0920 -1.81 0.0703
3 ChestCongestionYes 0.0993 0.0972 1.02 0.307
4 ChillsSweatsYes 0.192 0.127 1.51 0.132
5 NasalCongestionYes -0.220 0.114 -1.94 0.0534
6 SneezeYes -0.366 0.0983 -3.72 0.000213
7 FatigueYes 0.268 0.161 1.67 0.0959
8 SubjectiveFeverYes 0.444 0.103 4.30 0.0000192
9 HeadacheYes 0.00654 0.125 0.0522 0.958
10 WeaknessMild 0.0110 0.189 0.0580 0.954
# … with 24 more rowsThe symptoms with positive estimates predict higher body temperature and the negative estimates predict lower body temperature. No one symptom appears to be a strong predictor, and the some variables produced an NA.
Another way to look at the model without making predictions is using the glance function.
glance(ASlm_fit)# A tibble: 1 × 12
r.squ…¹ adj.r…² sigma stati…³ p.value df logLik AIC BIC devia…⁴ df.re…⁵
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
1 0.127 0.0851 1.14 3.06 4.24e-8 33 -1117. 2304. 2464. 911. 696
# … with 1 more variable: nobs <int>, and abbreviated variable names
# ¹r.squared, ²adj.r.squared, ³statistic, ⁴deviance, ⁵df.residualThe output shows various estimates of how well the model fits the data.
Compare linear models
To compare the models, we can use the compare_performance() function from the performance package.
compare_performance(RNlm_fit,ASlm_fit)# Comparison of Model Performance Indices
Name | Model | AIC (weights) | AICc (weights) | BIC (weights) | R2 | R2 (adj.) | RMSE | Sigma
-------------------------------------------------------------------------------------------------------
RNlm_fit | _lm | 2329.3 (<.001) | 2329.4 (<.001) | 2343.1 (>.999) | 0.012 | 0.011 | 1.188 | 1.190
ASlm_fit | _lm | 2303.6 (>.999) | 2307.3 (>.999) | 2464.4 (<.001) | 0.127 | 0.085 | 1.117 | 1.144The AIC and R2 are both estimates of how well the models fit the data by determining how much variation in the data is explained by the model. Considering the R2, the all symptom model is a better fit than the runny nose model because the R2 is higher. In addition, a better fitted model will have a lower AIC, which also supports the all symptom model as a better fit.
Fit logistic model: RunnyNose
Now we will consider nausea as our outcome of interest with runny nose as the predictor.
log_mod <- logistic_reg() %>% set_engine("glm") #sets logistic regression
RNlog_fit <- log_mod %>%
fit(Nausea ~ RunnyNose,
data = flu)
tidy(RNlog_fit)# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -0.658 0.145 -4.53 0.00000589
2 RunnyNoseYes 0.0502 0.172 0.292 0.770 The fitted model has produced a logistic equation of prob(Nausea) = 0.0502(RunnyNoseYes) -0.6578. This would indicate that having a runny nose increases the probability of having nausea.
Fit logistic model: All symptoms
Fitting the full model with all symptoms predicting nausea:
log_mod <- logistic_reg() %>% set_engine("glm")
ASlog_fit <- log_mod %>%
fit(Nausea ~ .,
data = flu)
tidy(ASlog_fit)# A tibble: 34 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.355 7.81 0.0454 0.964
2 SwollenLymphNodesYes -0.249 0.196 -1.27 0.203
3 ChestCongestionYes 0.268 0.211 1.27 0.203
4 ChillsSweatsYes 0.279 0.287 0.970 0.332
5 NasalCongestionYes 0.427 0.254 1.68 0.0931
6 SneezeYes 0.178 0.210 0.845 0.398
7 FatigueYes 0.229 0.372 0.617 0.537
8 SubjectiveFeverYes 0.273 0.225 1.22 0.224
9 HeadacheYes 0.333 0.285 1.17 0.242
10 WeaknessMild -0.118 0.447 -0.264 0.792
# … with 24 more rowsSimilar to the continuous outcome, the logistic regression estimates are positive if they increase the probability of having nausea and negative if they decrease the probability of having nausea.The same variables produced an NA in the model fitting.
Compare logistic models
We can once again compare the models using the compare_performance function.
compare_performance(RNlog_fit,ASlog_fit)# Comparison of Model Performance Indices
Name | Model | AIC (weights) | AICc (weights) | BIC (weights) | Tjur's R2 | RMSE | Sigma | Log_loss | Score_log | Score_spherical | PCP
-----------------------------------------------------------------------------------------------------------------------------------------------
RNlog_fit | _glm | 948.6 (<.001) | 948.6 (<.001) | 957.8 (>.999) | 1.169e-04 | 0.477 | 1.139 | 0.647 | -107.871 | 0.012 | 0.545
ASlog_fit | _glm | 819.5 (>.999) | 823.0 (>.999) | 975.7 (<.001) | 0.247 | 0.414 | 1.039 | 0.515 | -Inf | 0.002 | 0.658Following the same reasoning with the R2 and AIC that we used with the linear models, the all symptom model is a better fit of the data and explains more of the variation than the univariate model alone.